| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Talföljder - Serier
|
Serier |
En talföljd (följd) (en sekvens, en progression) är en ändlig eller oändlig följd av tal.
Talföljd kallas även serie i äldre litteratur.
a1, a2, a3, … an-1, an, an+1, …
Talen a (an) kallas talföljdens element eller talföljdens term.
Talföljden kan betraktas som en funktion sådan att mot varje positivt heltal n svarar ett bestämt tal an.
Talföljden a1, a2, …, an, … tecknas ofta kortare ![]()
Talen i följden behöver inte ha olika värden, t ex 1, 2, 1, 2, 1, 2, …
För vissa talföljder kan elementen an beräknas ur föregående element genom en formel som då kallas en rekursionsformel.
T.ex.: an = an-1 + 3 (… 4, 7, 10, 13 …)
En talföljd är
växande, om an+1 ≥ an
och strängt växande om an+1 > an för alla n,
avtagande, om an+1 ≤ an och strängt avtagande om an+1 < an för alla n,
monoton, om den är antingen växande eller avtagande,
oändlig, om n kan anta hur stora värden som helst,
begränsad upptill, om det finns ett tal M, sådant att an < M för alla n,
begränsad nedtill, om det finns ett tal m, sådant att an > m för alla n
Konvergent - divergent
Om talen i en oändlig talföljd närmar sig ett bestämt tal b, kallas talföljden konvergent, och b kallas talföljdens gränsvärde. En följd, som inte är konvergent, kallas divergent.
Talföljden 1/2, 1/4, 1/8, … är konvergent med gränsvärdet 0;
-1, 1/2, -1/3, 1/4, … är konvergent med gränsvärdet 0;
1, 0, 1, 0, 1, 0, … är divergent;
11, 22, 33, … är divergent.
En (oändlig) decimalutveckling är en konvergent talföljd. Betrakta t.ex. det rationella talet ![]() och dess decimalutveckling 0,757575 …; den senare står för den konvergeta följden 0,7, 0,75, 0,757, 0,7575, …, vars gränsvärde är
och dess decimalutveckling 0,757575 …; den senare står för den konvergeta följden 0,7, 0,75, 0,757, 0,7575, …, vars gränsvärde är ![]() .
.
En talföljd, sådan att differensen mellan ett element och närmast föregående är konstant. En aritmetisk talföljd är given genom an = a1 + (n - 1) · d, varvid d kallas differensen.
Exempel: 5, 8, 11, 14, …, 5 + (n - 1)·3, …
Summan az elementen a1, a1+d, a1+2d, …, a1+(n-1)d i en aritmetisk talföljd kallas en aritmetisk summa (eller aritmetisk serie).
Geometrisk talföljd
En talföljd, sådan att kvoten mellan ett element och närmast föregående är konstant. En geometrisk talföljd är given genom an = a1·q n-1, varvid q kallas kvoten.
Exempel: 1/2, 1/4, 1/8, 1/16, … 1/2n
Summan av elementen a1, a1q, a1q2, … a1qn-1 i en geometrisk talföljd kallas en geometrisk summa (eller geometrisk serie).
Fibonacci-följden
Följden 1, 1, 2, 3, 5, 8, 13, … där varje tal är summan av de båda närmast föregående (definierad av rekursionsformeln fn = fn-1 + fn-2, n ≥ 3, med begynnelsevärdena
f1 = f2 = 1).
När n växer mot ∞, går fn-1/fn mot ![]() , som är proportionen i gyllene snittet.
, som är proportionen i gyllene snittet.
Serier
Om a1, a2, …, an är en följd av tal så kallas a1 + a2 + a3 + … + an för en serie.
En serie betecknas med vanligen Σan. Elementen i talföljden kallas seriens termer.
Om serien är ändlig med n termer, så skrivs den:
a1 + a2 + a3 + … + an = ![]()
Om serien är oändlig skrivs den: a1 + a2 + a3 + … =![]()
I det senare fallet definieras delsumman (partialsumman) av de n första termerna som sn = a1 + a2 + a3 + … + an.
Ändliga serier
Aritmetiska summan
En serie, där differensen mellan två på varandra följande termer är konstant, sägs vara aritmetisk.
ai = ai-1 + d an = a1 + (n - 1) d
Om a1 är första termen och d differensen, blir serien: a1 + (a1 + d) + (a1 + 2d) + … + (a1 + (n - 1)d).
Summan av termerna är:
![]()
| Sn | = | a1 | + | (a1+d) | + | (a1+2d) | + | … | + | (an-2d) | + | (an-d) | + | an | [summan] |
| Sn | = | an | + | (an-d) | + | (an-2d) | + | … | + | (a1+2d) | + | (a1+d) | + | a1 | [summan i omvänt ordning] |
| 2·Sn | = | (a1+an) | + | (a1+an) | + | (a1+an) | + | … | + | (a1+an) | + | (a1+an) | + | (a1+an) | [ 2·summan = n·(a1+an)] |
Aritmetiska serier av n:te ordningen. Dessa kännetecknas av att n:te differensserien har alla termerna lika [(n+1):te differensserien har alla termerna = 0]. En differensserie bildas ur en serie genom att man tar skillnaden mellan på varandra följande termer.
| Serien: | 2 | + | 9 | + | 28 | + | 65 | + | 126 | + | 217 | + | 344 | + | 513 | |
| 1:a differensserien: | 7 | + | 19 | + | 37 | + | 61 | + | 91 | + | 127 | + | 169 | |||
| 2:a differensserien: | 12 | + | 18 | + | 24 | + | 30 | + | 36 | + | 42 | |||||
| 3:a differensserien: | 6 | + | 6 | + | 6 | + | 6 | + | 6 | |||||||
| 4:a differensserien: | 0 | + | 0 | + | 0 | + | 0 |
Summan av en aritmetisk serie av n:te ordningen
| Betrakta serien | a0+a1+a2+a3+ … + ak |
| 1:a differensserien betecknas: | a0(1)+a1(1)+a2(1)+a3(1)+ … + ak-1(1) |
| 2:a differensserien betecknas: | a0(2)+a1(2)+a2(2)+a3(2)+ … + ak-2(2) |
| osv. | |
| n:te differensserien betecknas: | a0(n)+a1(n)+a2(n)+a3(n)+ … + ak-n(n) |
| (n+1):a differensserien | =0 + 0 + … + 0 |
binomialkoefficienter ![]() se hos kombinationer
se hos kombinationer
Ex.: Beräkna ![]()
| Serien: | 1 | + | 4 | + | 9 | + | 16 | + | 25 | + | … | + | k2 |
| 1:a differensserien | 3 | + | 5 | + | 7 | + | 9 | + | … | + | (2k-1) | ||
| 2:a differensserien | 2 | + | 2 | + | 2 | + | … | + | 2 |
Serien är av 2:a ordningen.
(%i1)
sum (v^2,v,1,k);
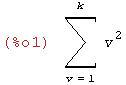
(%i2)
sum (v^2,v,1,k), simpsum;
![]()
Geometriska summan
En serie, där kvoten mellan två på varandre följande termer är konstant, sägs vara geometrisk.
Den har alltså formen: a + aq + aq2 + … + aqn-1.
Summan är:
![]()
| Sn | = | a | + | aq | + | aq² | + | … | + | aqn-1 | [summan] | ||
| q·Sn | = | aq | + | aq² | + | … | + | aqn-1 | + | aqn | [q·summan] | ||
| q·Sn-Sn | = | -a | + | 0 | + | 0 | + | … | + | 0 | + | aqn | [ (q - 1)·summan = aqn - a ] |
Sn(q - 1) = aqn - a
Oändliga serier
Om delsummorna Sn = a1 + a2 + a3+ … + an har ett gränsvärde S då n → ∞, säger man att serien är konvergent med S, annars är den divergent. Om Sn oscillerar mellan olika värden, kallas serien oscillerande.
Ex.:
Den oändliga geometriska serien a + aq + aq2 + … + aqn + … konvergerar om |q| < 1 och divergerar, om |q| > 1.
I första fallet är dess summa ![]() på grund av att i
på grund av att i ![]() gäller att qn → 0.
gäller att qn → 0.
Den harmoniska serien ![]() divergerar.
divergerar.
I en harmonisk följd bildar termernas inverterade värden en aritmetisk följd.
Benämningen är lånad från musiken. För att en sträng må efter hand giva tre tonerna av en durtreklang (C, E, G) måste de vibrerande längderna förhålla sig som 1/4, 1/5, 1/6, och dessa tals reciproka värden, 4, 5, 6 är en aritmetisk progression.
En alternerande serie (dvs. en serie med omväxlande positiva och negativa termer) är konvergent, om termerna är monotont avtagande dvs. an ≥ an+1 ≥ an+2.
En serie är absolut konvergent, om serien av termernas absoluta belopp är konvergent.
Potensserier
En serie av formen a0 + a1x + a2x2 + a3x3 + … + anx n + … kallas potensserie. Den konvergerar, då |x| < r, där r ett positivt tal (seriens konvergensradie). Det område, där |x| < r, har nämligen formen av en cirkel med radien r i den Gausska komplexa talplanet. Är x reellt, utgörs området av intervallet -r < x < r.
r fås ur följande gränsvärde:
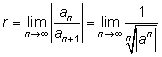 om dessa existerar.
om dessa existerar.
T.ex.:
Serien ![]() har konvergensradien 1, på grund av att
har konvergensradien 1, på grund av att ![]()
Serien ![]() konvergerar för alla x, på grund av att
konvergerar för alla x, på grund av att ![]()
Taylorserie
För utveckling av en funktion i potensserie gäller följande formel:
![]()
där Rn kallas (Lagranges) restterm och
![]()
![]()
Några potensserier
| Funktion | Serieutveckling | Konvergencia | ev. anmärkn. |
| Binomialserier | |||
| (1 + x)n | |x| < 1 | ||
| (1 ± x)-1 | |x| < 1 | ||
| (1 ± x)½ | |x| ≤ 1 | ||
| Exponentialserier | |||
| ex | |x| < ∞ | Det är en Maclaurin expansion of ex. Det konvergerar till ex för alla värden av x |
|
| e | = 2,71828182846... | ||
| cosh x = |
|x| < ∞ | ||
| sinh x = |
|x| < ∞ | ||
| ax = ex ln a | |x| < ∞ | ||
| Logaritmiska serier | |||
| ln(1 + x) | -1 < x ≤ 1 | ||
| ln(1 - x) | -1 ≤ x < 1 | ||
| ln x | 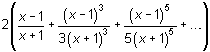 |
x > 0 | |
| Trigonometriska funktionernas serier | |||
| sin x | |x| < ∞ | ||
| cos x | |x| < ∞ | ||
(%i1)
taylor(exp(x),x,0,7);
![]()
(%i2)
taylor(cosh(x),x,0,9);
![]()
(%i3)
taylor(sin(x),x,0,9);
![]()
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |