WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

En trigonometrisk ekvation är en ekvation där den obekanta förekommer som argument i en trigonometrisk funktion. På grund av trigonometriska funktionernas periodicitet har trigonometriska ekvationerna vanligen oändligt många lösningar.

Man kallar för lösningar eller rötter sådana värdena av x, som satisfierar ekvationerna.

sin x = a
har reella lösningar om |a| ≤ 1, och den allmänna lösningen är:

eller i grader:

där k är ett godtyckligt heltal (k = 0; ±1; ±2; ±3 …).

sin x = sin x₀ är sann om och endast om x = x₀ + 2kπ eller x = - x₀ + (2k + 1)π

De flesta moderna symbolhanterande program kan lösa trigonometriska ekvationer:
t.ex. MuPad: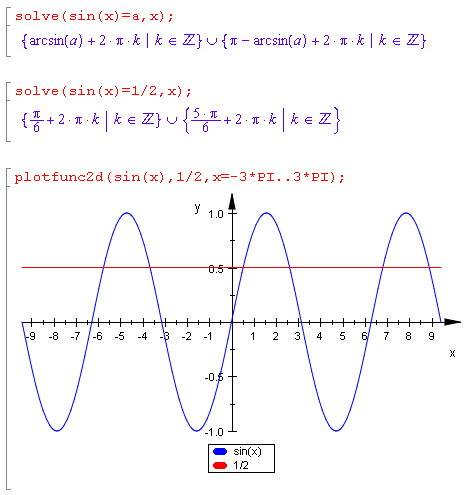

cos x = a
har reella lösningar om |a| ≤ 1, och den allmänna lösningen är:

cos x = cos x₀ är sann om och endast om x = x₀ + 2kπ eller x = - x₀ + kπ.

tan x = a
har lösningar om a inte är rent imaginärt tal, och den allmänna lösningen är:

tan x = tan x₀ är sann om och endast om x = x₀ + kπ och argumenten (2k + 1) är uteslutas.

Typuppgifter

1. sin x (1 + 2 cos x) = 0.
Lösning:

a) sin x = 0, x₁ = kπ,

b) 1 + 2 cos x = 0, cos x = - , x₂ = ± + 2 kπ.

2. tan 3x cos x = 0
Lösning:

a) tan 3x = 0, 3x = kπ, x₁ = k

b) cos x = 0, x₂ = (2k + 1); dessa lösningar är uteslutas eftersom tan 3x₂ = tan är oändligt.

3. sin 7x = sin 5x
Lösning:

a) 7x + 5x = (2k + 1)π, 12x = (2k + 1)π, x₁ = (2k + 1)

b) 7x - 5x = 2kπ, 2x = 2kπ, x₂ = kπ

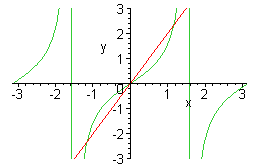
För de flesta trigonometriska ekvationer finns det inga enkla allmänna lösningsmetoder. Även de som ser sig ganska enkla ut (t.ex. tan x = 2x) kan man lösa bara grafiskt eller med numeriska metoder.